Simple Logic Neuron

This is based on a class exercise involving using a simple neuron to model a few basic logic functions (AND, OR, XOR).
This model applies logic 0/1 inputs and uses them to attempt to train the model to predict logic values. Here are diagrams for a each logic function (red means '1' is the output, blue means '0'):
ANDORXOR

Discussion

AND and OR case

Neural networks are designed to take a set of weighted inputs and use them to predict an output state. In this case we are using inputs in the range [0,1] to predict an output of 0 or 1.


The AND case is simple:
Level 1 WeightsLevel 1 BiasLevel2 WeightsLevel2 Bias
[-5.6573, -5.7037][8.0903][-14.9732][6.5046]

The steps are:
  1. X[0] is multipliex by -5.6576 and added to X[1] multiplied by -5.70
  2. That result has a bias of 8.0903 added.
  3. That result is put through a sigmoid activation function.
  4. That result is multiplied by -14.9732
  5. That result has 6.5 added to it
  6. That result is put through a sigmoid activation function.

Mapping it out for 3 of 4 cases and reducing to two decimal places:
X[0]=0, X[1]=0X[0]=1, X[1]=0 (0,1 case is similar) X[0]=1, X[1]=1
  • X[0]*-5.65 + X[1]*-5.70 = 0
  • 0 + 8.10 = 8.10
  • sigmoid(8.10) =~ 1
  • 1 *-14.97 = -14.97
  • -14.97 + 6.5 = -8.47
  • sigmoid(-8.47) = 0, what we expect
  • X[0]*-5.65 + X[1]*-5.70 = -5.65
  • -5.65 + 8.10 = 2.45
  • sigmoid(2.4) =~ 0.91
  • 0.91 *-14.97 = -13.62
  • -13.62 + 6.5 = -7.12
  • sigmoid(-7.12) = 0, what we expect
  • X[0]*-5.65 + X[1]*-5.70 = -11.36
  • -11.36 + 8.09 = ~-4
  • sigmoid(-4) = 0
  • 0.0*-14.97 = 0
  • 0+ 6.5 = 6.5
  • sigmoid(6.5) = 1, what we expect


    • XOR case

    The XOR case is harder... the AND case could be modeled as: 
    sigmoid(X * [ 5,5] - 5)
    with [1,1] yielding sigmoid(10-5) =~ 1 and the others equaling 0.
    Likewise the OR case could be modeled as: 
    sigmoid(X * [ 5,5] - 0)
    with [1,0] yielding sigmoid(5) or [1,1] yielding sigmoid(10) =~ 1 and the [0,0] case equaling 0.
    Technically the result goes through another sigmoid function at the output. but there's no other opportunity for X to influence the result. This means the XOR case is tricky because you have two numbers which could add up to a '1' but, if both are '1' should (but don't) add up to a '0'.
    The solution is to use two neurons: 
    (sigmoid(X * [ 5,5] - 0) - 1*sigmoid(X * [ 5,5] - 5))   essentially (X[0] OR X[1]) - (X[0] AND X[1])

    Code Repository

    My Github holds the python scripts.

    How to use

    ./SimpleLogicNeurons.py

    returning (numbers may change slightly): 
    Should be  1  was  0.46285498
XOR with 1 neuron should FAIL:  FAIL
OrderedDict([('linear1.weight', tensor([[-8.6583, -9.2757]])), ('linear1.bias', tensor([1.5032])), ('linear2.weight', tensor([[-8.0780]])), ('linear2.bias', tensor([-0.1426]))])
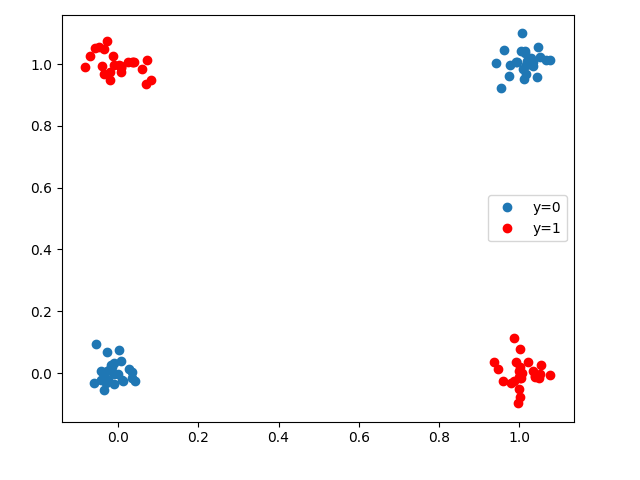
 XOR with 2 neurons should PASS: PASS
OrderedDict([('linear1.weight', tensor([[-7.3292, -7.5733],
        [-5.9858, -6.1268]])), ('linear1.bias', tensor([3.2565, 9.0655])), ('linear2.weight', tensor([[-13.7802,  13.4591]])), ('linear2.bias', tensor([-6.4077]))])
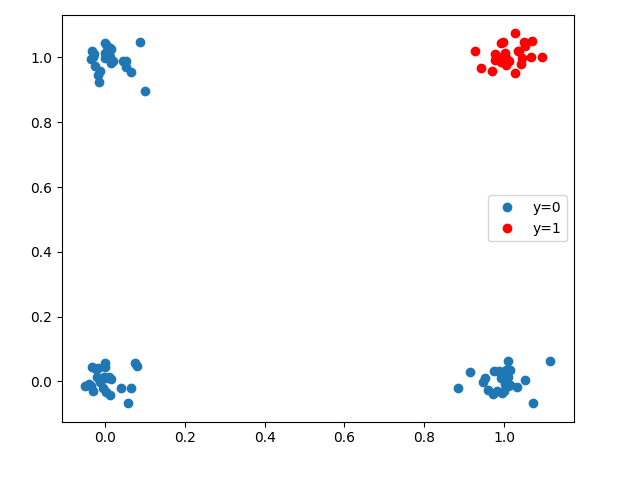
AND should PASS:         PASS
OrderedDict([('linear1.weight', tensor([[-5.6573, -5.7037]])), ('linear1.bias', tensor([8.0903])), ('linear2.weight', tensor([[-14.9732]])), ('linear2.bias', tensor([6.5046]))])
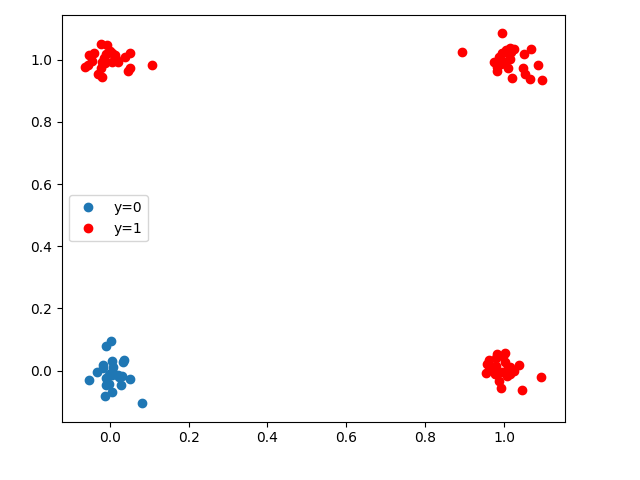
OR should PASS:         PASS
OrderedDict([('linear1.weight', tensor([[6.6210, 6.6750]])), ('linear1.bias', tensor([-3.4170])), ('linear2.weight', tensor([[14.3268]])), ('linear2.bias', tensor([-6.4032]))])